Rombusz Átlói

A rombusz egy olyan négyszög, amely paralelogramma, megtartja annak összes tulajdonságát, de emellett egyenlő oldalú. Mivel a rombusz minden oldala egyenlő, és a paralelogramma tulajdonságaiból adódóan az ellentétes szögei is egyenlőek egymással, a rombusz átlói nemcsak hogy egy pontban metszik egymást, amely két egyenlő részre osztja őket, hanem mindig merőlegesek is lesznek egymásra.

Amikor átlókat húznak egy rombuszban, négy egybevágó derékszögű háromszögre osztják, amelyek szárai az átlók felei. Bármelyik ilyen derékszögű háromszögben, ismerve az átfogót (a rombusz oldala), számítsa ki mindkét szárat. E célra a szinusz és koszinusz trigonometrikus arányait használják a derékszögű háromszögben - mivel mindkét szár a és b, ismeretlen, a számításokhoz szükség lesz a háromszög egyik hegyesszögére.

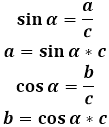
E képletek rombusz paramétereire való átváltásához szükséges a háromszög oldalait a rombusz oldalaihoz és átlóihoz, valamint a háromszög hegyesszögét a rombusz szögeihez kapcsolni.

A rombusz oldala, ahogy megegyeztünk, a háromszög átfogója lesz, és az átlók felei veszik fel a szárak szerepét. Ezután fordított sorrendben, a teljes átlók megtalálásához minden kiszámított szárat meg kell kétszerezni.

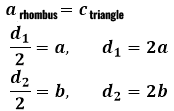
A szinusz és koszinusz használatához a rombusz átlóinak és szárainak meghatározásához használt szög nem más, mint a rombusz szögének fele, mivel a rombusz átlói a szögeinek felezői. Ezért a következő egyenlőség lesz igaz:

Most a rombusz átlóinak általános képletének levezetéséhez az oldala és szöge alapján (egyébként a hegyes vagy tompaszög választása nem befolyásolja a számítási eredményeket) a leírt helyettesítéseket be kell helyettesíteni az eredeti háromszög képleteibe, ahonnan a számítási algoritmus kezdődött.

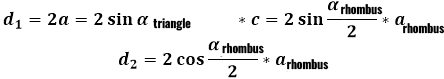
A számítások fordított elvégzése után a rombusz oldalát az átlókon vagy a rombusz oldalai közötti szögön keresztül is megtalálhatja.