Egyenlő szárú háromszög magassága
Egy egyenlő szárú háromszöget olyan háromszögnek neveznek, ahol a három oldal közül kettő egyenlő egymással. Az egyenlő oldalakat a háromszög a oldalainak nevezik, a harmadik oldalt b az egyenlő szárú háromszög alapjának nevezik.
Ennek megfelelően ilyen háromszögben három magasság húzható, amelyek közül kettő egyenlő egymással, hasonlóan az oldalakhoz - ezek a magasságok a háromszög a oldalára esnek, és a harmadik magasság az alapra esik. A háromszög magassága a háromszög szögéből az ellenkező oldalra húzódik derékszögben. A legtöbb probléma, amely a háromszög magasságával kapcsolatos, az általa alkotott derékszögű háromszögeken keresztül oldható meg.
Vizsgáljuk meg az egyes eseteket külön-külön.
Az egyenlő szárú háromszög magassága, amely az alapra esik, számos egyedi tulajdonsággal rendelkezik, amelyek nem alkalmazhatók más magasságokra ilyen háromszögben. Különösen, az egyenlő szárú háromszög alapjára húzott magasság egybeesik a súlyvonallal és szögfelezővel, amely az alapra húzódik, ezért nemcsak derékszöget alkot az alappal, hanem két egyenlő részre osztja azt, mint egy súlyvonal, és hasonlóan két egyenlő részre osztja a szöget, mint egy szögfelező. Ennek eredményeként a magasság a háromszög egyfajta szimmetriatengelye, és két egybevágó derékszögű háromszögre osztja azt. Ilyen háromszögben a magasság egy befogó, és a hosszának megtalálásához az egyenlő szárú háromszög oldalait a derékszögű háromszög oldalaihoz kell viszonyítani. Az egyenlő szárú háromszög oldala lesz az átfogó, és a második befogó meghatározásához az egyenlő szárú háromszög alapját félbe kell osztani, a súlyvonal tulajdonsága alapján.
Az egyenlő szárú háromszög magasságának hossza egyenlő a Püthagorasz-tétellel a négyzetgyökével az egyenlő szárú háromszög oldalának négyzete és az egyenlő szárú háromszög alapjának négyzetének negyede összegének:
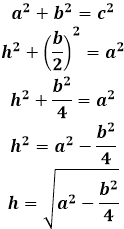
A második eset, amikor a feladat feltételei szerint az egyenlő szárú háromszög oldalára eső magasságot kell megtalálni, a legegyszerűbben a háromszög területén keresztül tárul fel.
Bármely háromszög területe többféleképpen is meghatározható - például a háromszög három oldalán keresztül Heron képletével, vagy a magasságon keresztül, megszorozva azzal az oldallal, amelyre esik. Mindkét módszer azonos területértékeket eredményez, így mindkét képlet egyenlővé tehető, és innen levezethető a végső képlet az egyenlő szárú háromszög oldalára eső magasságra.
Heron képlete egy egyenlő szárú háromszögre némileg egyszerűsített formát ölt az oldalak ismétlődése miatt:
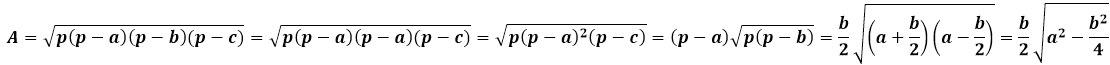
Egyenlő Szárú Háromszög Terület az oldalra eső magasságon keresztül
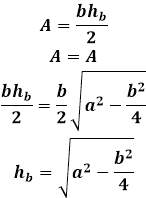
Ugyanez a képlet használható bármely magasság megtalálására egy egyenlő szárú háromszögben, ha a megfelelő oldalakat cseréljük a képletben.
Egy egyenlő szárú háromszög magasság képlete az oldalon keresztül és az alapnál lévő szög α: h=a sinα
Képlet az oldalon keresztül és az alapnál lévő szöggel szemben β:
![]()
Képlet az alapon keresztül és az ott lévő szöggel α:
![]()
az alapon keresztül és az azzal szemben lévő szöggel β:
![]()