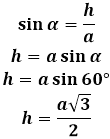Egyenlő oldalú háromszög magassága

Egy egyenlő oldalú háromszög egy szabályos sokszög (egy geometriai alakzat, ahol minden szög és minden oldal egyenlő). Valójában ez jelentősen leegyszerűsíti bármely, az ilyen háromszöget jellemző paraméterek kiszámításának folyamatát, beleértve a magasságot is.

Egy egyenlő oldalú háromszögben mindhárom magasság egyenlő hosszúságú, így bármelyik megtalálásával az összes vonalra alkalmazhatjuk az kapott értéket. Ráadásul az összes magasság teljesen egybeesik mindhárom súlyvonallal, szögfelezővel és szimmetriatengellyel, más néven medián. A három vonal metszéspontja rendelkezik a magasságok, a súlyvonalak és a szögfelezők metszéspontjának tulajdonságaival, egyben képviselve bármelyik lehetséges háromszög középpontját, beleértve a beírt és köré írt kör középpontját is.

Ebből kiindulva, egy egyenlő oldalú háromszög magasságának megtalálásához bármilyen ismert paramétert használhatunk, például a háromszög oldalát.

Egy egyenlő oldalú háromszög magassága, amely bármely oldalra húzódik, egy derékszögű háromszöget alkot benne, amelyet trigonometriai összefüggésekkel lehet számítani, mivel ismert, hogy egy egyenlő oldalú háromszögben minden szög 60 fokos. Az így kapott derékszögű háromszögben a magasság lesz az egyik befogó, a 60 fokos szöggel szemben, és az egyenlő oldalú háromszög oldala lesz az átfogó, ennek megfelelően a magasság megtalálásához a szinuszt kell alkalmazni. Ha 60 fokot helyettesítünk az alfa szögbe, kiderül, hogy az egyenlő oldalú háromszög magassága az oldal felének és a három négyzetgyökének szorzata.