Pitagorasz-tétel

A Pitagorasz-tétel az euklideszi geometria alapvető összefüggése, amelyre számos következmény és más tétel épül, amelyek a Pitagorasz-tételből származtathatók. A VI században született, a tétel egyszerű egyenlettel kapcsolja össze a derékszögű háromszög oldalait, és számos bizonyítéka van, amelyek közül az egyik egyesíti az algebrát és a geometriát.

A Pitagorasz-tétel szerint a derékszögű háromszögben vannak befogók a és b – ezek a derékszöggel szomszédos oldalai, és a négyzeteik összege adja az átfogó négyzetét – a háromszög harmadik oldala, a derékszöggel szemben.

Ezt bizonyítani lehet négy derékszögű háromszög felépítésével, úgy, hogy mindegyik hosszú befogója a következő háromszög rövid befogója legyen, a szögek csúcsai egybeesve.

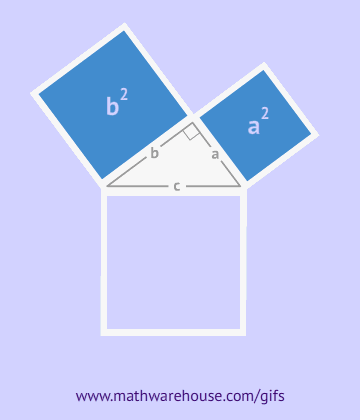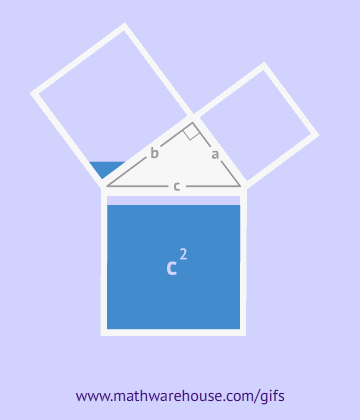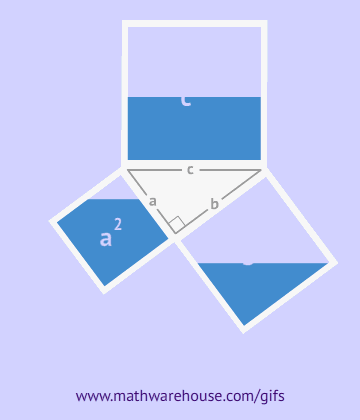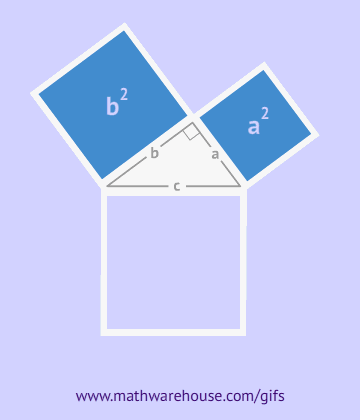
Amint az ábrából látható, az egész alakzat egy négyzetet alkot oldalával c, amely egyúttal ezen háromszögek átfogója, és ennek az alakzatnak a területe egyenlő c², a négyzet területének képlete szerint. Ezen négyzet mellett négy derékszögű háromszög is található, amelyek területe , a közepén egy másik kis négyzet található. A kis négyzet oldala a befogók különbségével egyenlő, így területe ennek a különbségnek a négyzetével egyenlő lesz. (a-b)²=a²-2ab+b²

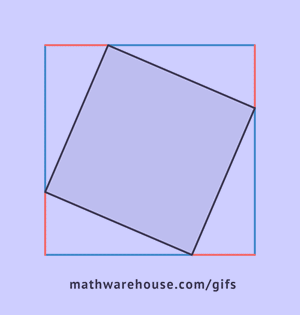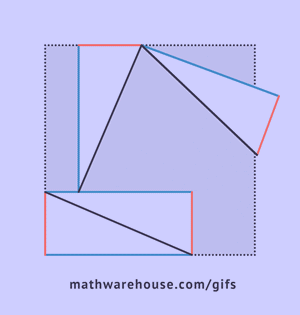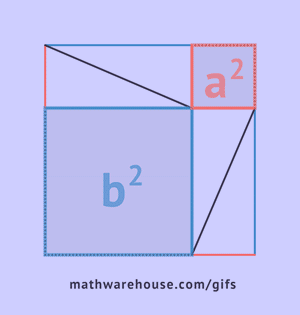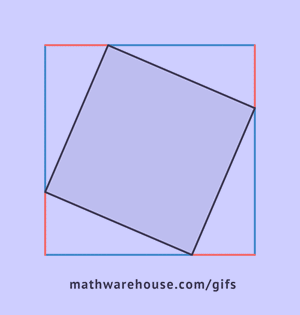
Képzeljük el a nagy négyzet területét a kis négyzet és négy háromszög területeinek összegeként a szuperpozíció elve szerint.

Így a négyzet területe egyszerre egyenlő az átfogó négyzetével és a befogók négyzeteinek összegével, amit be kellett bizonyítani. a²+b²=c²