Mátrix transzponálása

A transzponált mátrixot úgy kapjuk meg, hogy az eredeti mátrix sorait oszlopokra vagy oszlopait sorokra cseréljük.

A mátrix transzponálásának tulajdonságai:
Kétszer transzponált mátrix megegyezik az eredeti mátrixszal A^TT(A^T)^T=A
A mátrix összegének transzponáltja egyenlő az összeget képző mátrixok transzponáltjának összegével (A + B)^T=A^T+B^T
A szorzat transzponáltja egyenlő a tényezők transzponáltjainak szorzatával, fordított sorrendben (A × B)^T=A^T×B^T

Transzponált mátrix eléréséhez az eredeti mátrixszal a következő műveletek egyikét kell végrehajtani:

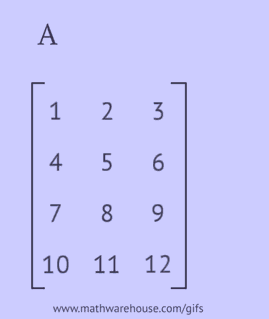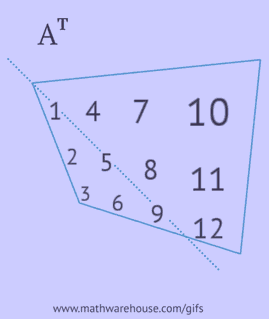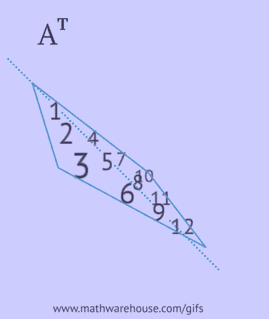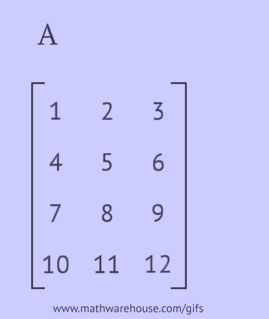
- írja le minden sorát azonos sorrendben oszlopként;
- írja le minden oszlopát azonos sorrendben sorba;
- tükrözze elemeit a főátló mentén, a bal felső saroktól kezdve, és jobbra és lefelé haladva, amíg el nem éri az alsó vagy jobb szélt.

A transzponált mátrixokra átalakított mátrixokat az algebrai egyenletrendszerek megoldására, az inverz mátrix megtalálására, valamint a lineáris algebra más feladataiban is használják.