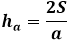삼각형의 높이

임의의 삼각형에서 (모든 변의 길이가 다른 경우), 변에 그려진 높이 , 중선 그리고 이등분선 는 완전히 다른 선을 나타냅니다. 삼각형에서 높이를 찾기 위해 정삼각형이나 이등변 삼각형의 중선이나 이등분선의 속성을 사용할 수 없으므로 다른 방법을 사용해야 합니다.

유사한 방법 중 하나는 삼각형의 일반적인 매개변수인 면적을 사용하는 것입니다. 계산 알고리즘은 이등변 삼각형의 면적이 높이를 통해 찾을 수 있다는 사실을 기반으로 합니다. 삼각형의 세 변을 알고 있을 때, 헤론의 공식을 사용하여 면적을 찾고 다른 면적 공식을 사용하여 높이를 표현할 수 있습니다.헤론의 공식을 사용한 면적, 그리고 다른 면적 공식을 사용하여 그것을 통해 높이를 표현합니다.

헤론의 공식을 사용하여 삼각형의 면적을 계산하려면 먼저 삼각형의 반주변을 계산해야 합니다. 이름 그대로 반주변은 세 변의 길이의 합을 둘로 나눈 것입니다.

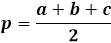
면적 공식 자체는 반주변과 각 변과의 차이의 곱으로, 전체 표현식이 제곱근 아래에 있습니다.

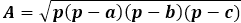
다른 한편으로, 높이를 통한 동일한 삼각형의 면적은 삼각형의 변과 그에 내린 높이의 곱의 절반에 해당합니다. 따라서 높이는 면적을 두 배로 나눈 후 삼각형의 변으로 나눈 값과 같습니다. 이전 공식에서 삼각형의 세 변을 통한 면적을 표현하여 높이 공식에 대입할 수 있습니다.

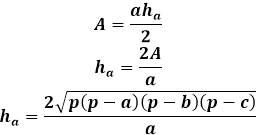
이 높이 공식은 이등변, 정삼각형, 또는 이등각 삼각형에 적용할 수 있으며, 다른 것이 없는 경우에도 적용됩니다.

삼각형의 세 변을 알고 있을 때 높이를 계산하는 데는 면적 공식을 사용하는 긴 과정이 필요합니다. 면적을 통해 표현된 삼각형의 높이는 그것이 내린 변과만 관련이 있으므로, 계산기와 수동 계산에서 적절한 변을 높이 공식에 대입하기 위해 변의 순서를 정확히 표시하는 것이 매우 중요합니다.

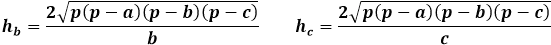
임의의 삼각형의 높이 공식