Ortócentrum — a háromszög magasságainak metszéspontja

A háromszög ortocentrumának megtalálásához használhatja a kalkulátort, ahol meg kell adnia a koordinátákat. Automatikus módban a számítások képletekkel történnek. Az összes számítást manuálisan is elvégezheti.

Például, az alábbi adatpontok állnak rendelkezésre:
A – 4,3;
Ban – 0,5;
Valamivel– 3,-6.
Az első dolog, amit meg kell találni, az oldalak meredeksége, amelyet - jelöl m , a következő képlet használatával:

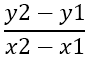
Ebből következik:

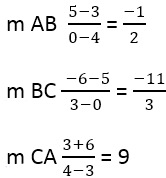
Ezután meg kell találni a merőleges oldalak meredekségét, ehhez a képletet használják:

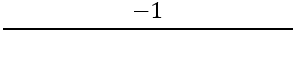
Van:
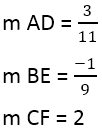Amikor a merőlegesek meredeksége megtalálható, használhatja az egyenesek egyenletét, például az AD, ahol a pont 4,3, és a meredekség 3/11:

Egyszerűsítéssel megkaptuk: 3x - 11y=-21
Az VE egyenesre, ahol a pont 0,5, és a meredekség -1/9, megkapjuk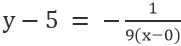

Az egyszerűsítés adja: x+9y=45.
És az utolsó egyenesek CF, ahol a pont 3, -6, és a meredekség 2, megkapjuk az egyenletet y+6 = 2(x-3).
És egyszerűsítés, 2x — y = 12.
Ha megoldja a három egyenletből kettőt, megtalálhatók az x és y értékek. Ehhez a példához:
x értéke = 8,05263;
y értéke = 4,10526.
Amelyek ebben az esetben a keresett Ortócentrum koordinátái.