Gyökvonásos Középeltérés
Két, három, négy és több szám gyökvonásos középeltérése. Ez a szórás, gyökvonásos középeltérés, gyökvonásos közép, átlagos négyzetes, szórás — a valószínűségelmélet és a statisztika szerinti véletlen változó értékeinek szórásának mutatója a matematikai várakozáshoz képest.
Általában a felsorolt kifejezések egyenlők a variancia négyzetgyökével.
Példa a szórás kiszámítására a következő képletek segítségével:
Számítsuk ki a diák átlagos jegyét: 2; 4; 5; 6; 8.
Cátlagos jegy a következő lesz:
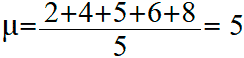
Számítsuk ki a jegyek átlagos értékétől való eltéréseinek négyzeteit:
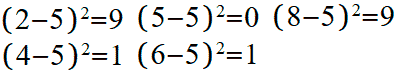
Számítsuk ki az átlagos aritmetikai értéket (variancia) ezeknek az értékeknek:
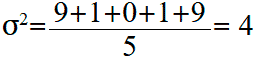
A szórás egyenlő a variancia négyzetgyökével:
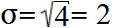
Ez a képlet csak akkor érvényes, ha ez az öt érték az általános népességre vonatkozik. Ha ezek az adatok egy nagyobb népességből származó véletlen minták (például öt véletlenszerűen kiválasztott diák jegyei egy nagyvárosból), akkor a variancia kiszámításához használt képlet nevezőjében n = 5 helyett n − 1 = 4:
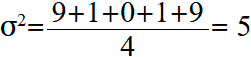
Akkor a szórás a következő lesz:
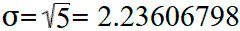
Ezt az eredményt a variancia torzítatlan becslése alapján számított szórásnak nevezzük. Az osztás n − 1 helyett n torzítatlan becslést ad a varianciára a nagy általános népességek esetében.
Számítsuk ki a diák átlagos jegyét: 2; 4; 5; 6; 8.
Cátlagos jegy a következő lesz:
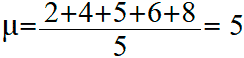
Számítsuk ki a jegyek átlagos értékétől való eltéréseinek négyzeteit:
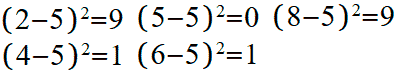
Számítsuk ki az átlagos aritmetikai értéket (variancia) ezeknek az értékeknek:
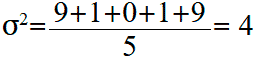
A szórás egyenlő a variancia négyzetgyökével:
Ez a képlet csak akkor érvényes, ha ez az öt érték az általános népességre vonatkozik. Ha ezek az adatok egy nagyobb népességből származó véletlen minták (például öt véletlenszerűen kiválasztott diák jegyei egy nagyvárosból), akkor a variancia kiszámításához használt képlet nevezőjében n = 5 helyett n − 1 = 4:
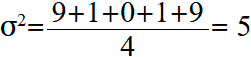
Akkor a szórás a következő lesz:
Ezt az eredményt a variancia torzítatlan becslése alapján számított szórásnak nevezzük. Az osztás n − 1 helyett n torzítatlan becslést ad a varianciára a nagy általános népességek esetében.