Pythagorase teoreem

Pythagorase teoreem on fundamentaalne seos Eukleidese geomeetrias, millele tugineb suur osa Pythagorase teoreemist tuletatud kõikidest tagajärgedest ja muudest teoreemidest. See tuletati VI eKr. sajandil, teoreem seob täisnurkse kolmnurga küljed lihtsa võrrandiga ja sellel on mitmeid tõestusi, millest üks ühendab nii algebrat kui geomeetriat.

Vastavalt Pythagorase teoreemile on täisnurkse kolmnurga kaatetid a ja b – need on nurgaga külgnevad küljed ja nende ruutude summa annab hüpotenuusi ruudu – kolmnurga kolmas külg, mis asub täisnurga vastas.

Seda saab tõestada, konstrueerides neli täisnurkset kolmnurka nii, et nende pikk kaatet oleks järgmise kolmnurga lühike kaatet, nurkade tipud langevad kokku.

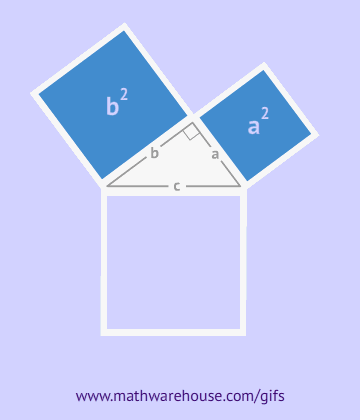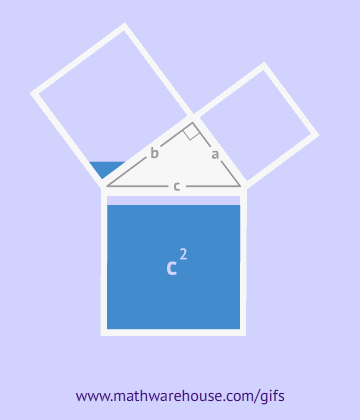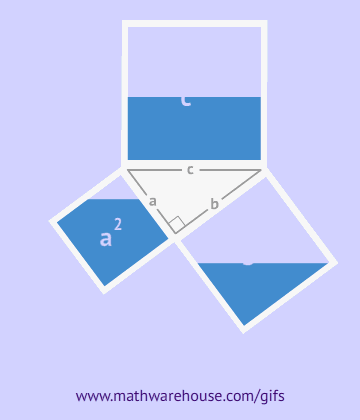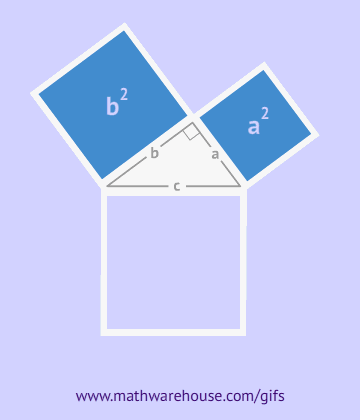
Nagu jooniselt näha, kujutab kogu kuju endast külje c, olles samal ajal nende kolmnurkade hüpotenuus, ruutu ja selle kuju pindala on võrdne c², vastavalt ruudu pindala valemile. Lisaks sellele ruudule sisaldab see neli täisnurkset kolmnurka pindalaga 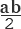, selle keskel on veel üks väike ruut. Väikese ruudu külg võrdub kaatetite erinevusega, seetõttu on selle pindala võrdne selle erinevuse ruuduga. (a-b)²=a²-2ab+b²

Esitame suure ruudu pindala väikese ruudu ja nelja kolmnurga pindalade summana vastavalt superpositsiooni põhimõttele.

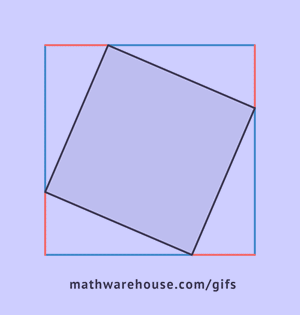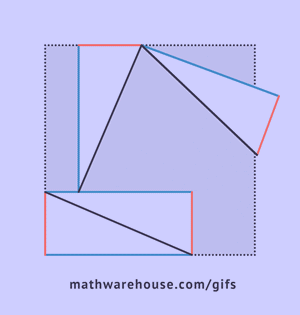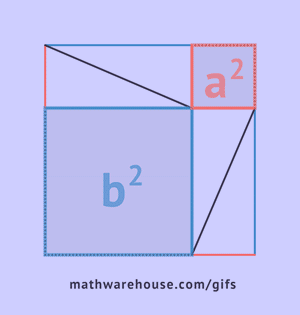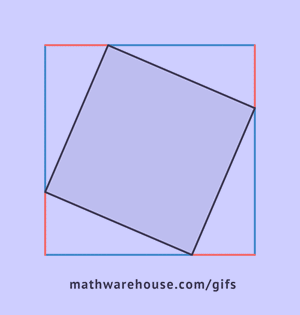
Seega on ruudu pindala samaaegselt võrdne hüpotenuusi ruuduga ja kaatetite ruutude summaga, mis tuli tõestada. a²+b²=c²